Heisenberg's uncertainty principle

The previous example showed that the electrons within a wave have an unknown location, it's somewhere there but we can't exactly define it precisely.

Physicist Werner Heisenberg came up with an astonishing theory, it considers that all the physical magnitudes of the macroscopic world are not measurable simultaneously on a microscopic scale, in particular, the quantities whose product is homogeneous to an action, more precisely the position and the momentum on one hand and the energy and Time on the other hand: such quantities are said to be incompatible and are subjected to the integralities of Heisenberg: 

𝝙P.𝝙x ⩾ h/2𝚷;                     𝝙E.𝝙t⩾ h/2𝚷;

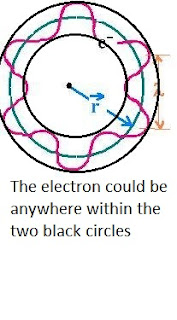
Since this principle has no interest at the macroscopic scale, then let's take an example of something microscopic, in this case, an electron that is situated in its fundamental state (the closest orbital to the nucleus). Let's consider the following data: the atomic ray r = 0.53 Ǻ , V= 2,2 . 10 exp(6) m/s and the velocity variation 𝝙V/V = 10%

By applying Heisenberg's Integrality

𝝙P.𝝙x ⩾ h/2𝚷;   𝝙r ⩾ h/ 2𝚷.𝝙P;      or 𝝙P = m 𝝙V;

𝝙r ⩾ 6,62.10 exp(-34) . 100 / 2𝚷. 9.10exp(-31) . 2,2.10exp(6) ==> 𝝙r= 5.26Ǻ.

which leads to r1 = (0,53± 5,26) Ǻ.

We can conclude that it's impossible to know the position and the velocity at the same time, the electron could exist anywhere in the stated interval.

I bet you didn't understand anything from all the bullshit I said. Let's try to make things more fluent by returning to the roots of the trouble which is something behaving as a particle and as a Wave and examining each concept separately.

Being a particle is very easy to understand, a particle has a defined location it's like tracing a car's movement by a GPS, you know where it is it is 100% in that location and 0% everywhere else.

Waves, on the other hand, are more delicate to comprehend. If we drop something in a stable water surface the shock will cause a disturbance generating circular waves that propagate, but there is no doubt that waves aren't something you can give an exact location, they are all over the place! But at least we can identify some features like amplitude and more importantly the wavelength. As the wave disseminates the ups and downs are constantly variating and if we visualize a single spot on the surface of the water we can see that it suddens some ups and downs depending on the wave motions.

What I am trying to say is that the notion is quite probabilistic meaning that at a very specific moment we can encounter either a peak or a valley.A wavelength has the probability to be in a lot of different spaces.

Now let's link things together, relying on the Luis de Broglie equation 𝞴=h/mV, by a simple mathematical reasoning 𝞴 decreases when m or V increase and vice versa.

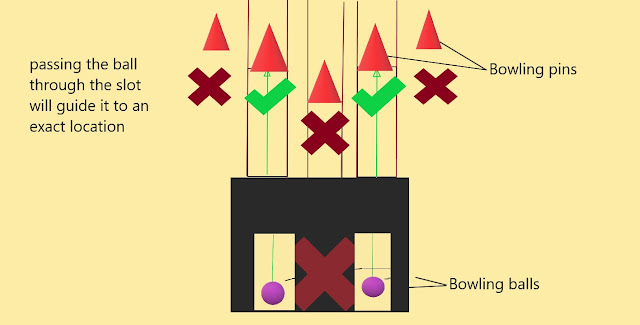
Knowing that an electron's wave length is big enough to be measured, we can determine its momentum, but the position remains unknown it's inexistent. Contrariwise, if we know a particle's position, but it doesn't have a wavelength so we don't know its momentum. You have to look at this a binary system containing two variables where we should mix the 2 equations to determine them.

To get a particle with both position and wavelength, we need to make a graph that has waves (wavelength) but only in a small area (position). How to do that?

It's nothing else than giving our object some possibilities, by attributing different wave lengths which mean different momentums. 

By overlapping the possible wavelengths we get places where the pics line up which gives us a bigger wave, and places where the peaks of ones fill the valleys of the others. The result has regions where we see peaks and other regions with nothing at all. The interesting thing is the more we add possibilities by attributing more and more wavelengths, the smaller the peak regions and the bigger the other regions become.By tending the number of possibilities to the infinity we minimize the peak region and somehow obtain a clear wavelength in a small region. The result is a quantum object with both a momentum and wavelength!!! Surely we lose a lot of certainty by attributing possibilities.

So let's sum up this **** :

𝝙P.𝝙x ⩾ h/2𝚷

If we want to reduce the position uncertainty, we have to rely on a smaller wave packet add more waves which is a bigger momentum uncertainty so if 𝝙x increases, 𝝙P decreases.

On the other hand, if we want to reduce the momentum uncertainty 𝝙P, we have to lower the wavelengths number, therefore, deploy a bigger wave packet which means a bigger position uncertainty 𝝙x. 

Final conclusion: 𝝙x and 𝝙P work dependently where each one corrects the error of the other maintaining the term superior to h/2𝚷.

Hope that breaks your mind as it did to mine :D